
前言
遗传算法的一些思路我在开篇有提到一些,这里给出具体过程: 1、生成两个种群,分别使用BL算法和BL_plus算法; 2、开始迭代 3、调用两个种群的update_max()函数更新最优个体 4、如果两个种群中有最优解(也就是12家店铺全部铺上去了),则跳出循环,返回该个体; 5、如果达到迭代次数,则跳出循环,返回两个种群的最优个体; 6、如果达到交换迭代次数,则: 假设种群P1的最优个体适应值为fbest1,P2的最优个体适应值为fbest2 (1)若fbest1>fbest2,则用P1的最优个体替换P2的最劣个体; (2)若fbest1<fbest2,则用P2的最优个体替换P1的最劣个体; 7、对两个种群分别进行选择、交叉、变异
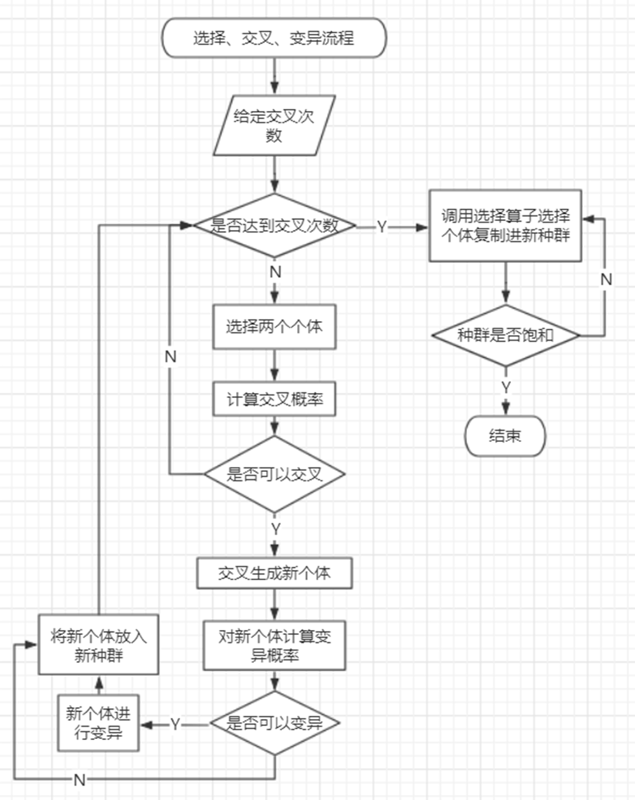
8、更新两个新种群的最优个体 9、若新种群最优个体的适应值小于旧种群最优个体适应值,则用旧种群的最优个体替换新种群的最劣个体。
核心代码
/// <summary>
/// 遗传算法
/// </summary>
/// <param name="path">店铺数据位置</param>
/// <param name="w">地区宽度</param>
/// <param name="h">地区高度</param>
/// <param name="iterations">迭代次数</param>
/// <param name="size">种群大小</param>
/// <param name="change">交换迭代次数</param>
/// <param name="crossover_frequency">交叉频率</param>
/// <param name="Pc1">用于计算交叉概率的参数一</param>
/// <param name="Pc2">用于计算交叉概率的参数二</param>
/// <param name="Pm1">用于计算变异概率的参数一</param>
/// <param name="Pm2">用于计算变异概率的参数二</param>
/// <param name="op_int">在基因片段一上的交叉算子</param>
/// <param name="op_bool">在基因片段二上的交叉算子</param>
/// <param name="va_int">在基因片段一上的变异算子</param>
/// <param name="va_bool">在基因片段二上的变异算子</param>
/// <returns>最优个体</returns>
public static Individual Inheritance(string path, int w, int h, int iterations, int size, int change,
double crossover_frequency, double Pc1, double Pc2, double Pm1, double Pm2, operator_int op_int,
operator_bool op_bool, variation_int va_int, variation_bool va_bool)
{
Population pop1 = new Population(path, w, h, size, "BL");
Population pop2 = new Population(path, w, h, size, "BL_plus");
int fbest;
for (int iteration = 0; iteration < iterations; iteration++)
{
pop1.update_max();
pop2.update_max();
fbest = pop1.fmax > pop2.fmax ? pop1.fmax : pop2.fmax;
Console.WriteLine("第{0}次迭代,最优解的适应度为:{1}", iteration, fbest);
if (pop1.Fmax.character.Count == 12)
{
return pop1.Fmax;
}
if (pop2.Fmax.character.Count == 12)
{
return pop2.Fmax;
}
if ((iteration + 1) % change == 0)
{
int min_index_1 = pop1.find_min_index();
int min_index_2 = pop2.find_min_index();
if (pop1.fmax > pop2.fmax)
{
pop2.ind[min_index_2] = pop1.Fmax;
pop2.update_max();
}
else if (pop1.fmax < pop2.fmax)
{
pop1.ind[min_index_1] = pop2.Fmax;
pop1.update_max();
}
}
int crossover_times = (int) (size * crossover_frequency);
double cros_prob, r, var_prob;
Individual parent1, parent2;
List<Individual> new_ind = new List<Individual>();
List<int[]> gene_int;
List<bool[]> gene_bool;
//处理pop1
for (int i = 0; i < crossover_times; i++)
{
parent1 = pop1.ind[pop1.roulette()];
parent2 = pop1.ind[pop1.roulette()];
cros_prob = pop1.cros_probability(parent1, parent2, Pc1, Pc2);
r = Population.rand_double();
if (r <= cros_prob)
{
gene_int = op_int(parent1.gene_order, parent2.gene_order);
gene_bool = op_bool(parent1.gene_rotate, parent2.gene_rotate);
Individual child;
int[] ge_int;
bool[] ge_bool;
for (int j = 0; j < 2; j++)
{
child = new Individual(w, h, gene_int[j], gene_bool[j], "BL",
pop1.decode(gene_int[j], gene_bool[j]));
var_prob = pop1.mut_probability(child, Pm1, Pm2);
r = Population.rand_double();
if (r < var_prob)
{
ge_int = va_int(gene_int[j]);
ge_bool = va_bool(gene_bool[j]);
child = new Individual(w, h, ge_int, ge_bool, "BL",
pop1.decode(ge_int, ge_bool));
}
new_ind.Add(child);
}
}
}
while (new_ind.Count < size)
{
new_ind.Add(pop1.ind[pop1.roulette()]);
}
int index, fmax = 0;
for (int i = 0; i < size; i++)
{
if (new_ind[i].fit_count() > fmax)
{
fmax = new_ind[i].fit_count();
}
}
if (fmax < pop1.fmax)
{
index = 0;
int fmin = int.MaxValue;
for (int i = 0; i < size; i++)
{
if (new_ind[i].fit_count() < fmin)
{
index = i;
fmin = new_ind[i].fit_count();
}
}
new_ind[index] = pop1.Fmax;
}
pop1.ind = new_ind;
//处理pop2
new_ind = new List<Individual>();
for (int i = 0; i < crossover_times; i++)
{
parent1 = pop2.ind[pop2.roulette()];
parent2 = pop2.ind[pop2.roulette()];
cros_prob = pop2.cros_probability(parent1, parent2, Pc1, Pc2);
r = Population.rand_double();
if (r <= cros_prob)
{
gene_int = op_int(parent1.gene_order, parent2.gene_order);
gene_bool = op_bool(parent1.gene_rotate, parent2.gene_rotate);
Individual child;
int[] ge_int;
bool[] ge_bool;
for (int j = 0; j < 2; j++)
{
child = new Individual(w, h, gene_int[j], gene_bool[j], "BL_plus",
pop2.decode(gene_int[j], gene_bool[j]));
var_prob = pop2.mut_probability(child, Pm1, Pm2);
r = Population.rand_double();
if (r > var_prob)
{
ge_int = va_int(gene_int[j]);
ge_bool = va_bool(gene_bool[j]);
child = new Individual(w, h, ge_int, ge_bool, "BL_plus",
pop2.decode(ge_int, ge_bool));
}
new_ind.Add(child);
}
}
}
while (new_ind.Count < size)
{
new_ind.Add(pop2.ind[pop2.roulette()]);
}
fmax = 0;
for (int i = 0; i < size; i++)
{
if (new_ind[i].fit_count() > fmax)
{
fmax = new_ind[i].fit_count();
}
}
if (fmax < pop2.fmax)
{
index = 0;
int fmin = int.MaxValue;
for (int i = 0; i < size; i++)
{
if (new_ind[i].fit_count() < fmin)
{
index = i;
fmin = new_ind[i].fit_count();
}
}
new_ind[index] = pop2.Fmax;
}
pop2.ind = new_ind;
}
if (pop1.fmax > pop2.fmax)
{
return pop1.Fmax;
}
return pop2.Fmax;
}
最后
以上便是我寻找《开罗拉面店》最优解的全部过程啦!中间我走了很多弯路,甚至还准备了十几个参数准备拿来调参的,没想到才迭代了130多次就出结果了,非常幸运!不过其实也很好理解,因为按照我改进的算法生成的初始解,本来就离最优解不远,收敛速度快是很显然的。
最后贴上我找到的两个最优解:
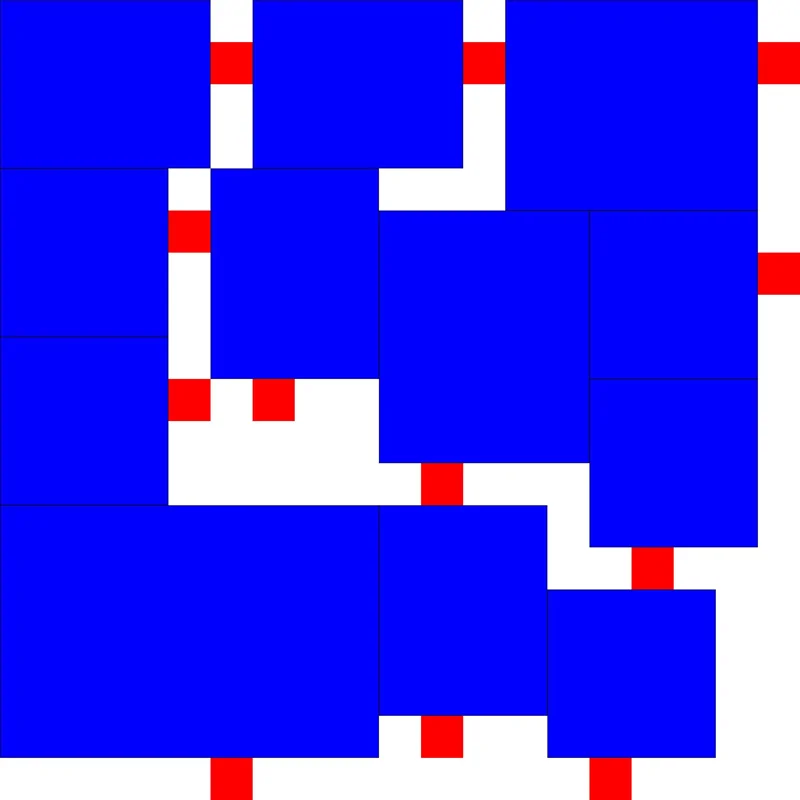
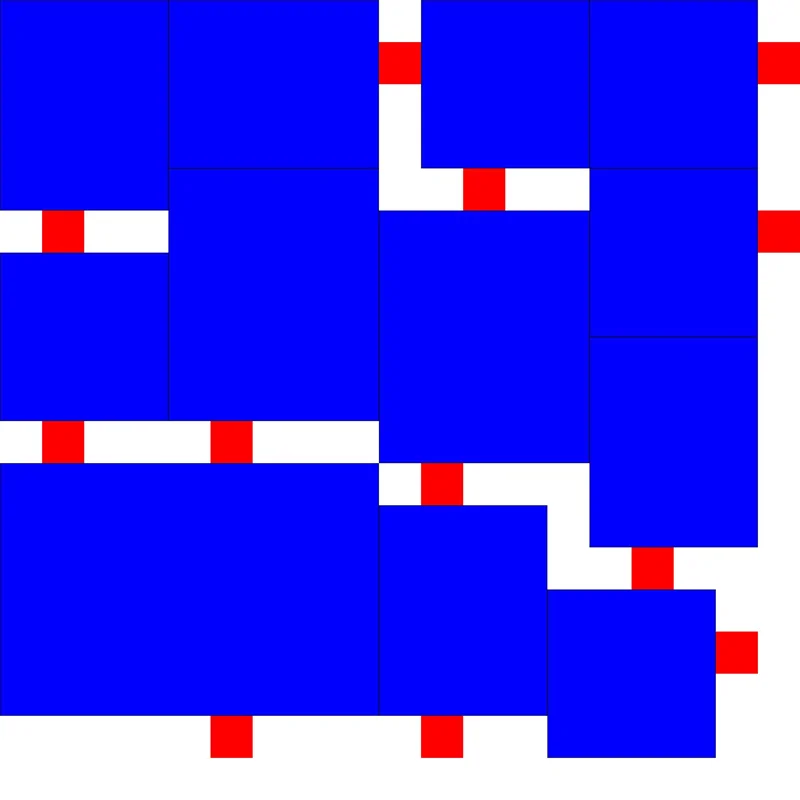
 程序设计实验室
微信公众号
程序设计实验室
微信公众号
