种群类:Population
属性
种群类首先要储存的便是上一篇中提到的原始基因;其次为了应用精英保存策略、择伏分配等,需要记录最优个体的相关信息;同时在计算交叉变异概率的时候,需要用到求平均适应值的方法,所以为了简化计算,储存每个个体的适应值是很有必要的。
/// <summary>
/// 个体列表
/// </summary>
public List<Individual> ind;
/// <summary>
/// 原始基因
/// </summary>
private List<Store> gene_pool;
/// <summary>
/// 最优个体
/// </summary>
public Individual Fmax;
/// <summary>
/// 最优个体适应值
/// </summary>
public int fmax;
/// <summary>
/// 最优个体对应索引
/// </summary>
public int fmax_index;
/// <summary>
/// 每个个体的适应值
/// </summary>
public int[] fit_count;
方法
更新最优个体,并更新适应度
在精英保存策略和择伏分配策略中,都需要找出种群最优个体,所以这里要做的就是更新最优个体的相关信息,顺便更新个体适应值。
/// <summary>
/// 更新种群最优个体,并更新适应度
/// </summary>
public void update_max()
{
int fit;
for (int i = 0; i < ind.Count; i++)
{
fit = ind[i].fit_count();
fit_count[i] = fit;
if (fit > fmax)
{
fmax_index = i;
fmax = fit;
Fmax = ind[i];
}
}
}
交叉概率
在我主要参考(白嫖)的那篇论文里,交叉概率是这样定义的:
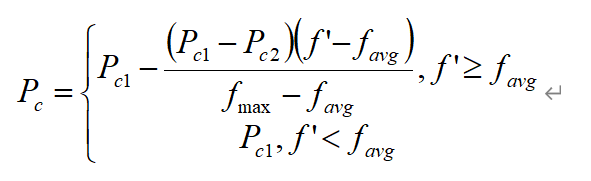
其中Pc1=0.9, Pc2=0.6, f'为参与交叉的两个个体中较大的适应值,favg为种群的平均适应值,fmax为种群的最大适应值。
为了求平均适应值,必须写一个小方法来计算,除此之外就是套公式了。
/// <summary>
/// 计算种群平均适应度
/// </summary>
/// <returns>平均适应值</returns>
public float avg()
{
float ans = 0;
foreach (var i in ind)
{
ans += i.fit_count();
}
return ans / ind.Count;
}
/// <summary>
/// 计算交叉概率
/// </summary>
/// <param name="ind1">个体一</param>
/// <param name="ind2">个体二</param>
/// <param name="Pc1">参数一</param>
/// <param name="Pc2">参数二</param>
/// <returns>交叉概率</returns>
public double cros_probability(Individual ind1, Individual ind2, double Pc1 = 0.9, double Pc2 = 0.6)
{
int fit1 = ind1.fit_count(), fit2 = ind2.fit_count(), f;
float fit_avg = avg();
update_max();
if (fit1 > fit2)
{
f = fit1;
}
else
{
f = fit2;
}
double ans = Pc1;
if (f >= fit_avg)
{
ans -= (Pc1 - Pc2) * (f - fit_avg) / (fmax - fit_avg);
}
return ans;
}
变异概率
变异概率的定义如下:
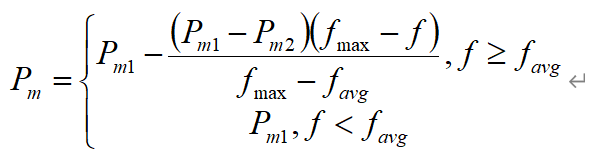
其中Pm1=0.1, Pm2=0.01, f为参与变异个体的适应值。
/// <summary>
/// 变异概率
/// </summary>
/// <param name="ind1">个体</param>
/// <param name="Pm1">参数一</param>
/// <param name="Pm2">参数二</param>
/// <returns>变异概率</returns>
public double mut_probability(Individual ind1, double Pm1 = 0.1, double Pm2 = 0.01)
{
int f = ind1.fit_count();
float fit_avg = avg();
update_max();
double ans = Pm1;
if (f >= fit_avg)
{
ans -= (Pm1 - Pm2) * (fmax - f) / (fmax - fit_avg);
}
return ans;
}
生成随机数
在交叉算子和变异算子中,要大量地用到生成一个随机整数;在轮盘赌算法以及遗传算法中,也要生成一个随机实数。
/// <summary>
/// 生成随机整数
/// </summary>
/// <param name="a">下限</param>
/// <param name="b">上限</param>
/// <returns>随机整数</returns>
public static int rand_int(int a, int b)
{
byte[] buffer = Guid.NewGuid().ToByteArray();
int iSeed = BitConverter.ToInt32(buffer, 0);
Random ran = new Random(iSeed);
return ran.Next(a, b);
}
/// <summary>
/// 生成(0,1)上的随机实数
/// </summary>
/// <returns>随机实数</returns>
public static double rand_double()
{
byte[] buffer = Guid.NewGuid().ToByteArray();
int iSeed = BitConverter.ToInt32(buffer, 0);
Random ran = new Random(iSeed);
return ran.NextDouble();
}
找到种群最劣个体
择伏分配策略中需要找出种群中的最劣个体。
/// <summary>
/// 找出最差个体对应索引
/// </summary>
/// <returns>最差个体对应索引</returns>
public int find_min_index()
{
int index = 0, fmin = int.MaxValue;
for (int i = 0; i < ind.Count; i++)
{
if (fit_count[i] < fmin)
{
index = i;
fmin = fit_count[i];
}
}
return index;
}
解码器
前面提到,解码器是将基因编码还原成基因的方法,由于是基于本种群的原始基因进行随机排序操作和随机旋转操作的,不需要改变原始基因本身,所以需要调用Store类的clone进行深复制,以保证原始基因的“纯洁”。
/// <summary>
/// 解码器,由两个基因片段编码生成个体的基因
/// </summary>
/// <param name="gene_order">基因片段编码一</param>
/// <param name="gene_rotate">基因片段编码二</param>
/// <returns>基因</returns>
public List<Store> decode(int[] gene_order, bool[] gene_rotate)
{
List<Store> ans = new List<Store>();
gene_pool.ForEach(i => ans.Add(i.Clone()));
for (int i = 0; i < gene_rotate.Length; i++)
{
if (gene_rotate[i])
{
ans[i].rotate();
}
}
return ans.OrderBy(e =>
{
var index = 0;
index = Array.IndexOf(gene_order, e.id);
if (index != -1)
{
return index;
}
return int.MaxValue;
}).ToList();
}
轮盘赌
轮盘赌算法是这样实现的:将每个个体的适应值进行归一化处理(也就是除以种群适应值总和),然后生成一个随机数,看看这个随机数落在哪个区间就选哪个个体。举例说明,比如有四个个体,适应值分别为1,2,3,4,归一化之后为0.1,0.2,0.3,0.4,我生成一个(0,1)上的一个随机实数r=0.61826,落在区间(0.1+0.2+0.3,0.1+0.2+0.3+0.4)上,所以选择了第四个个体。
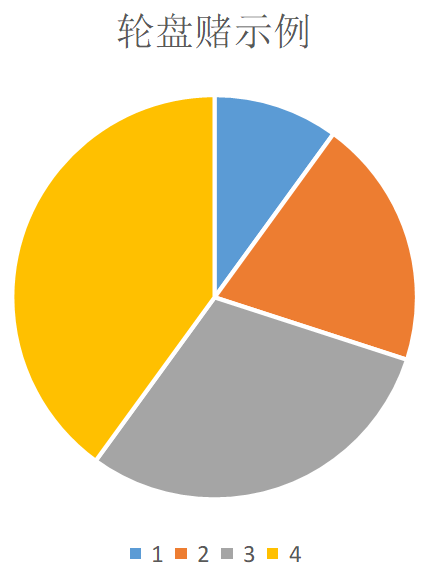
可以很直观地看出,适应值越大的个体,所占的扇形面积越大,也就越有可能被选中,这正是轮盘赌的目的——优胜劣汰,这有助于提高遗传算法的收敛速度,但又由其随机性,使得算法不容易陷入局部最优解。这便是遗传算法独特魅力的第一处体现。
还有一个要注意的点,为了保证最优个体的“纯洁”,尽量不破坏最优个体的结构,最优个体不参与轮盘赌。
/// <summary>
/// 轮盘赌算法,随机选择个体
/// </summary>
/// <returns>随机选择的个体</returns>
public int roulette()
{
Dictionary<int, double> dict = new Dictionary<int, double>();
for (int i = 0; i < ind.Count; i++)
{
if (i != fmax_index)
{
dict[i] = (double) fit_count[i] / (fit_count.Sum()-fmax);
}
}
double r = rand_double(), sum = 0.0;
int index = 0;
foreach (var k in dict)
{
sum += k.Value;
if (sum > r)
{
index = k.Key;
break;
}
}
return index;
}
 程序设计实验室
微信公众号
程序设计实验室
微信公众号
