前言

前段时间无聊回坑玩《开罗拉面店》，这是一款模拟经营类的小游戏，不管是画风还是游戏性都很对我胃口。

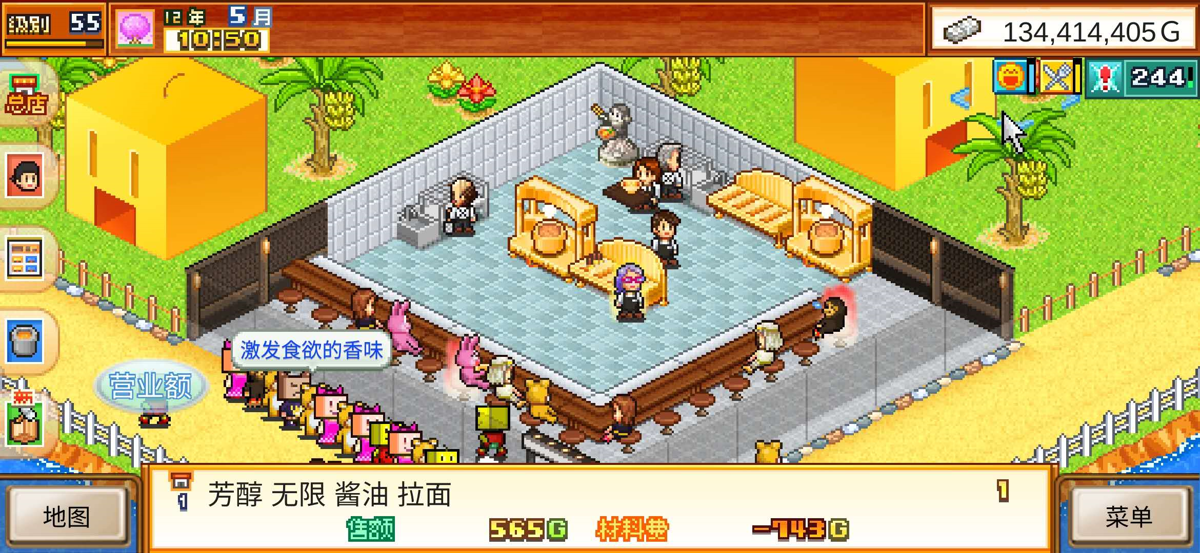
里面有一个玩法是拉面店布局，就给你一块地，还有几家店铺，你可以随便铺随便摆，当然肯定是摆的越多家店铺越好。

我一开始玩的时候也没想那么多，随便摆了摆就完事了，但玩到后期人气上不去，我就突发奇想，能不能把所有店铺摆进去？或者能不能尽可能多地去铺满这块地？

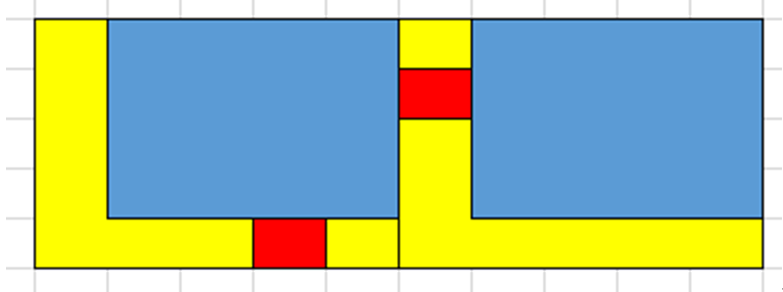
我就到处去找资料，然后有找到一个帖子是摆了11家店铺的（总共是12家店铺），地址：https://tieba.baidu.com/p/3583521915?red_tag=2365356271

这楼主就只是单纯的在excel上玩华容道拼图游戏，自己挪来挪去捣鼓出了这个布局，但这布局肯定不是最优的，因为这块地是19格*19格，也就是361格，然后12家店铺加起来也就274格，容错率特别高，也就是说12家店铺能全部放进去的可能性非常大。那要怎么找呢？

我先是学着楼主那样玩华容道，然后就发现这样效率贼低，因为有太多种布局了，一个一个试是找不出来的，而且也毫无规律可循。我又回忆起之前我捣鼓过的二维装箱问题，一细品就觉着，诶这不就是一个加了约束条件的二维装箱问题吗？？！！！！

于是我把这个问题当成算法题来看了。

引出问题

既然要当算法题来看，那肯定要把问题描述清楚了。现给出问题描述如下：

给定一块矩形格点区域，以及若干大小不同的拉面店，每家拉面店都是矩形格点块，而且每家拉面店都有一个入口，现在要求在满足以下约束条件的情况下，将这些拉面店填充到给定区域里。

约束条件：

  1. 拉面店在填充的时候，长边、宽边与矩形区域的长边、宽边所成的角度，要不是0°，要不是90°（也就是不考虑斜着插♂进去的情况）；
  2. 店铺与店铺之间不能重叠；
  3. 店铺不能超出矩形区域范围；
  4. 每家店铺的入口都存在一条路径可以通往矩形区域的边界；
  5. 店铺在填充的时候，严格嵌套在格点上，即店铺的四个顶点都在格点上；
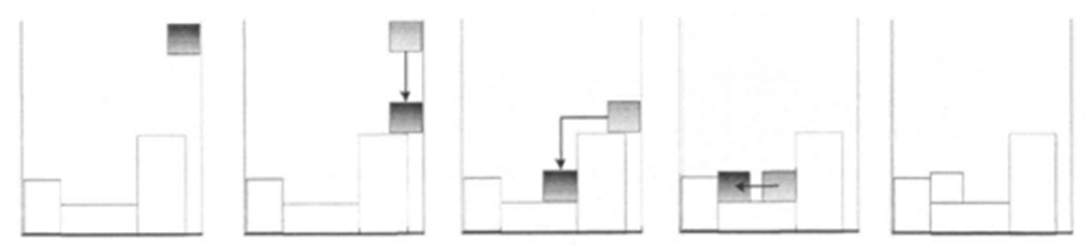
  6. 店铺的入口与店铺边界外接，入口只占一个格子，示例如下：

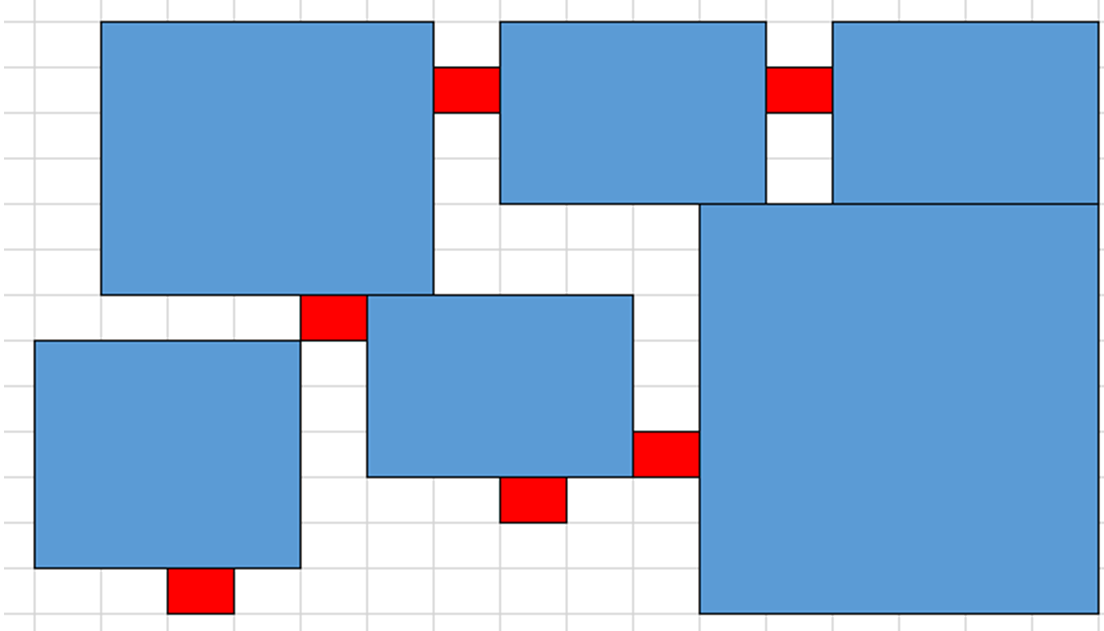
  1. 店铺可以旋转，不过旋转只能是绕着y=x（规定左为x轴正方向，下为y轴正方向）旋转，如图所示：

再强调一次，这个问题全部都是基于格子进行讨论的，接下来提到的点，指的是一个格子，而相对位置则是按格数来计算的，也就是向上几格向右几格，下移左移啥的也是按格子数移动的，诸如此类。

二维装箱问题

把问题描述清楚了，接下来就是与之相关的二维装箱问题了，我主要参考的是以下这篇论文：https://www.docin.com/p-902429329.html

这篇论文主要研究的是在有限宽无限高的矩形区域上的装箱问题，不过万变不离其宗，方法都是可以借鉴（白嫖）的，我主要研究的是BL算法和BL算法加强版，一个是因为这两个算法很好实现，比较简单，一个是考虑到这个问题的约束条件有点多，如果用贪心启发式算法或者递归算法，在判断约束条件4的时候都会特别困难，而在我看来约束条件4 是所有条件里最关键的，这也是我困扰了最久的一个地方。

先简单讲一讲BL算法。想象你在玩俄罗斯方块，然后给你的方块都是矩形的方块，每次你都是从右上角开始，你采取的放置方块的策略是：先不停地按下方向键，下到不能在下的时候按左，不停地按左方向键，左到不能再左的时候按下。。。 这样一直循环，直到不能同时往下和往左移动的时候停止，也就完成了这一方块的放置，可以放置下一个方块了。

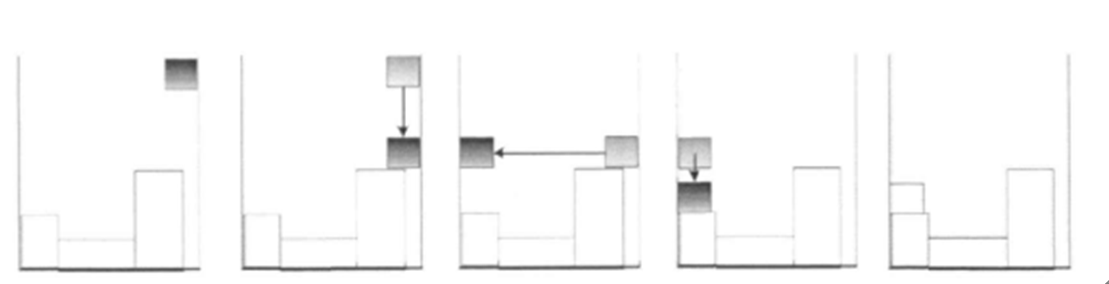
然后是改进的BL算法。同样是俄罗斯方块，同样是从右上角开始。你先疯狂按下方向键，下到不能再下的时候按左方向键，一点一点按，按到又可以往下的时候再按下方向键，有点像下楼梯，一直到不能同时往下或者往左的时候停止。

这两个算法满足了约束条件1、2、3、5，想要让这两个算法满足约束条件4、6、7，还需要做进一步的修改和改进。经过几个星期的摸爬滚打，我总算是找到了一个效果比较好的改进算法。

算法改进

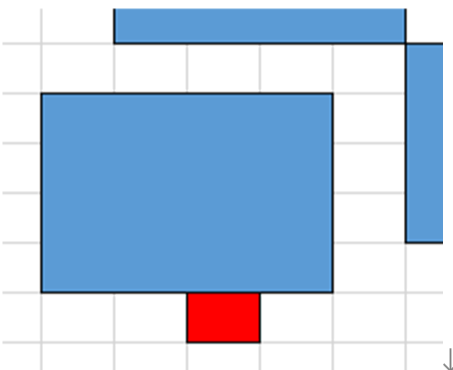
首先要考虑的问题是：怎么保证移动的过程中满足约束条件4，也就是怎么保证每一家店铺的入口都有路可以走到区域边界。我一开始考虑的是判断店铺有没有直接把门堵住，也就是直接覆盖了入口，如图所示：

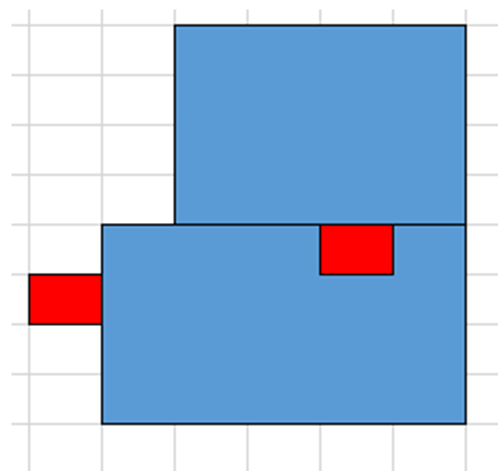
虽然这样肯定不行，我可以在遇到这种情况的时候后退一步，保证我的拉面店不会盖住别家的入口，但是我还是不能保证所有店的入口都有路，比如下面这种情况：

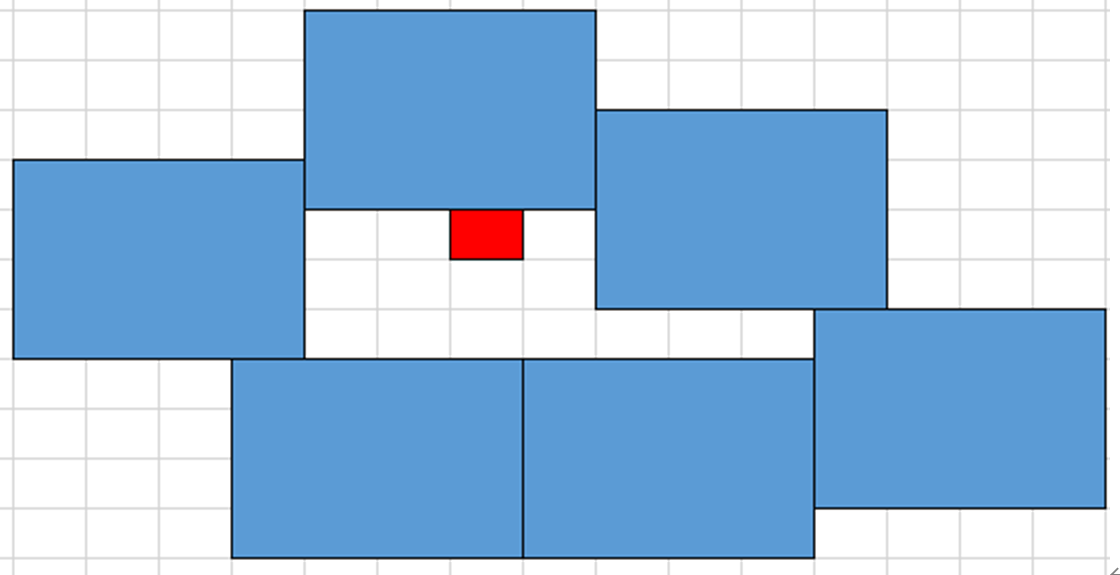
试问这么复杂的情况应该怎么判断这个入口有没有路呢？所以想要从堵住入口的情况去判断分析是行不通的。

考虑到约束条件7中店铺的旋转特点，店铺的入口只会分布在店铺的两条边上：

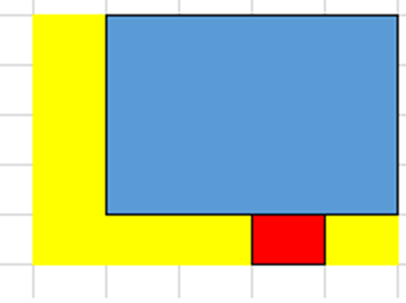
所以我只需要将店铺扩大一格，4x4变成5x5，然后再去铺，不管怎么铺都可以保证每家店的入口都有路可以通啦！而且这样操作简单，还能在不怎么改动算法的情况下使用那两个算法来摆放店铺，简直不要太机智！

但是这样有一个问题哦，这样浪费了好多空间，离最优解的距离有点远。为了尽可能靠近最优解，我对这两个算法进行了改进。在按原来的算法移动完这个店铺后，我再对这个店铺进行判断，往上移动一格，看看满不满足约束条件；往右移动一格，看看满不满足约束条件；同时往这两个方向移动一格，看看满不满足约束条件。这样子的话有五种情况：

1. 可以往上，但不能往右

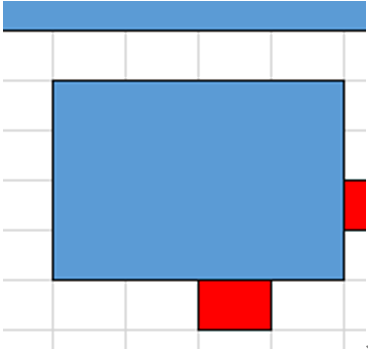这种情况往上移动。

2. 可以往右，但不能往上

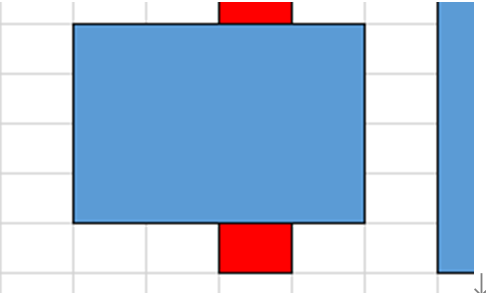这种情况往右移动。

3. 可以同时往两个方向移动

这种情况同时往两个方向移动。

4. 可以往上，也可以往右，但不能同时往两个方向移动

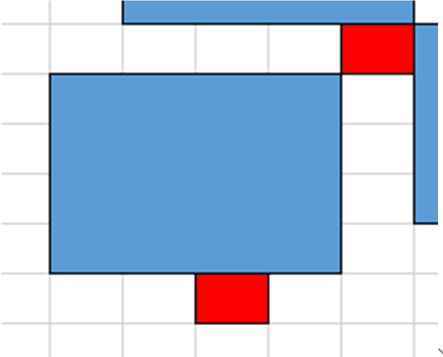这种情况选一个方向移动就行，我选的是往上移动。

5. 即不能往上，又不能往右

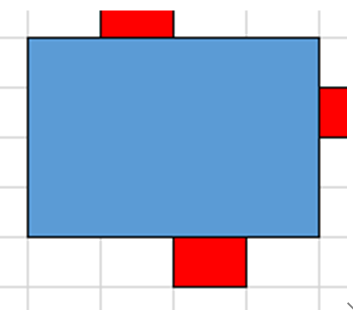这种情况就不移动了。

我让这些店铺无限循环判断并移动，直到出现情况5的时候退出循环，这样我这个店铺放置的位置应该就是没法再动了。

遗传算法

按照这个改进的两个算法，我可以生成一个比较理想的，也就是离最优解比较近的一个可行解。 接下来我只需要找到这些店铺的摆放顺序，还有哪些店铺是需要旋转的就行。要怎么找呢？随机搜索？暴力搜索？那也太费时间了吧！我的目光又回到了我主要用来参考的那篇论文，那篇论文使用的方法是启发式算法+遗传算法，于是我就在想：既然二维装箱问题可以用遗传算法来整，我能不能用遗传算法来找这个最优解呢？

于是我开始学习遗传算法的相关知识，经过长时间的摸索，我得出结论——可行！

网上有很多遗传算法的讲解，我就简单讲一讲我对这个算法的理解。

遗传算法是一个用来求最优解或者逼近最优解的算法，它主要是参考了自然界的优胜劣汰等法则，去随机地逼近最优解，进而找到最优解。

由于它的随机性，遗传算法不会陷入局部最优解，只需要加入一些简单的策略就可以跳出局部最优的情况；但也由于它的随机性，遗传算法的收敛速度会比较随机，可能你这次运行一下子就得到了比较理想的解，下次运行半天都很不理想；你也没办法保证每次运行的结果都是比较理想的，就有点像抽卡，你这次随机到的解比较靠近，你下次随机到的解可能就有点远了。

所以我在实现这个算法的时候还是很忐忑的，我完全不知道我能不能找到这个最优解，我只能寄希望于能尽可能逼近最优解了（好在最后我脸比较好，一发入魂，第一次运行只迭代了一百多次就得到最优解了，开心）

遗传算法有几个很关键的点：基因编码、选择、交叉、变异、适应度。

基因可以决定性状，这是一个一一映射的关系，联系到这道题，性状就是店铺的布局，而基因就是店铺的顺序以及每家店铺的旋转情况（旋转or没旋转），按照上面提到的改进后的算法，给定店铺的顺序以及店铺的旋转情况，可以确定唯一一个布局，显然是一一对应，所以可以将店铺的顺序以及旋转情况作为基因，布局作为性状。

选择要遵守优胜劣汰法则，优秀的个体要更能被选择到，常见的有轮盘赌、随机遍历、锦标赛等，我这里用的是轮盘赌。

传送门：https://blog.csdn.net/xinbolai1993/article/details/79458929

两个个体交叉生成一个新个体，应用到算法中的话就是由两个编码生成一个编码（或一对编码），这个生成的过程叫交叉算子。常见的交叉算子有PMX、OX、PBX、OBX、CX、SEC等，我是把这六个算子都实现了，本来想着一个一个试来调参的，结果试了第一个PMX就直接出结果了啊哈哈哈哈~

传送门：https://blog.csdn.net/ztf312/article/details/82793295

变异就比较简单了，变异算子是一个编码生成一个编码，也就是把编码里一些片段改一改，比如改一改顺序呀，或者false改为true啊之类的，至于片段要怎么选嘛，我参考了交叉算子里的OX和PBX，不多做赘述。

个体的适应度是用来评判个体的优秀程度的，关乎到个体被选择的概率大小。而在这道题中，优秀可以有多个指标，比如空间利用率大呀，或者铺好的店铺数量啊，这里我选择的是用铺好的每家店铺面积之和作为该个体的适应度。

遗传算法的大体流程是这样的：先生成初始种群，然后开始循环，计算每个个体的适应度，判断是否达到循环终止条件，是的话就跳出循环并输出最优解，否的话对种群中的个体进行选择、交叉、变异操作，生成新一代种群参与下一次迭代。

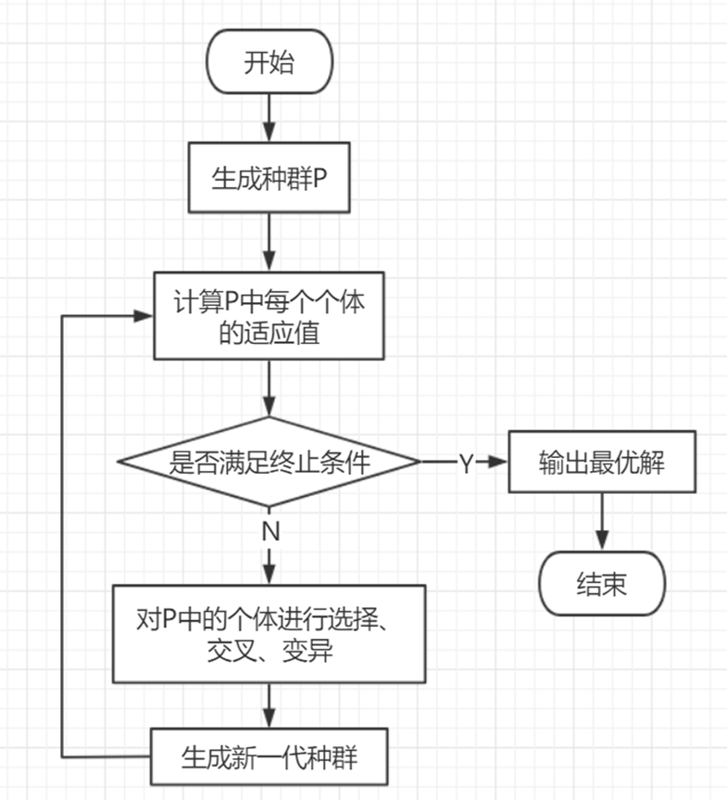
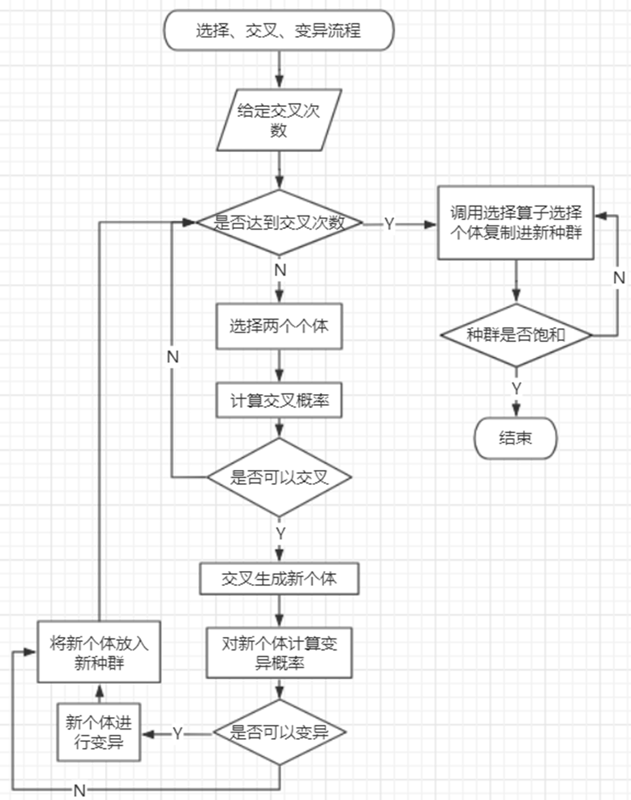
我在这个大体流程的基础上，参考（白嫖）了那篇论文里的使用两个种群来对比、精英保存策略、相比较择伏分配、交叉概率公式、变异概率公式、环形交叉、环形变异等思路。至于选择、交叉、变异的操作（那篇论文里没给），我的流程是给定交叉次数，每次交叉选择两个个体，计算交叉概率，可以交叉的话就交叉生成新个体，对新个体计算变异概率，可以变异的话变异，然后放入新种群，再从原始种群里选择个体复制进新种群，直到选满种群规模为止。

最后

至此，我要做的所有前期准备工作全部做好了，接下来就是直接敲代码！

PS：具体代码实现在下一篇，欢迎关注！